Ошибки первого и второго рода

Расчет издержек, вызванных неправильным назначением средств измерений. В большинстве нормативных документов, регламентирующих порядок назначения средств измерений, рекомендуется соотношение между погрешностью средств измерений и допуском контролируемого параметра равное 1/3. На практике данное соотношение часто не соблюдается. И выбирается средство или метод измерений с погрешностью больше нормированного соотношения. Увеличение погрешности измерений влечет за собой увеличение вероятности появление ошибок, то есть вероятность признания годного изделия дефектным и вероятность признания дефектного изделия годным (рисунок).

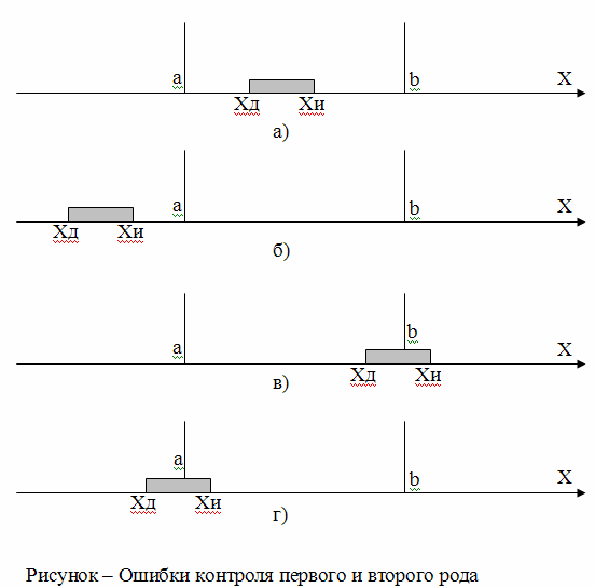
  Рисунок – Ошибки контроля первого и второго рода

Ситуация 1. Значения Хд – действительное значение контролируемого параметра и Хи – измеренное значение параметра в процессе контроля находятся в допускаемых пределах a,b (рисунок 29а). Указанное состояние контроля назовем гипотезой Н1. Вероятность этой гипотезы Р(Н1) – вероятность верного заключения о соответствии измеряемого значения допускаемому.

Ситуация 2. Значения Хд и Хи находятся вне поля допуска a,b (рисунок 29б). Вероятность гипотезы Р(Н2) – вероятность верного заключения о несоответствии измеряемого значения допускаемому.

Ситуация 3. Значение Хи указывает на брак, а Хд свидетельствует о годности (рисунок 29в). Вероятность гипотезы Р(Н3) – вероятность ложного брака или вероятность ошибки первого рода Р1.

 Ситуация 4. Значение Хи указывает на годность, а Хд свидетельствует о браке (рисунок 29г). Вероятность гипотезы Р(Н4) – вероятность пропуска бракованного изделия или вероятность ошибки второго рода Р2.

Вероятности гипотез Р(Н1), Р(Н2), Р(Н3), Р(Н4) несовместимы и образую полную группу событий (рисунок 30).

Р(Н1) + Р(Н2) + Р(Н3) + Р(Н4) = 1

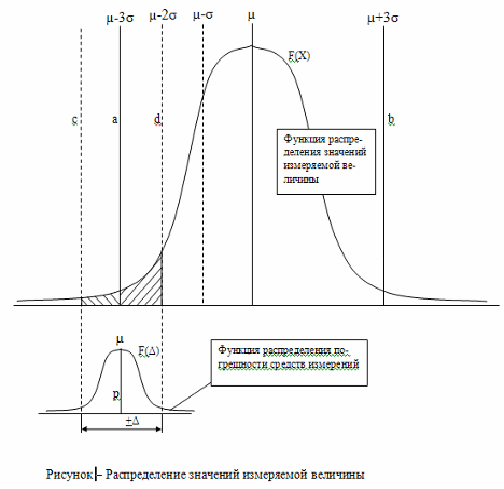
Рисунок – Распределение значений измеряемой величины

Теоретически величину ошибок первого рода можно рассчитать по формуле.

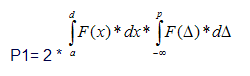
где F(x) – функция распределения значений измеряемой величины (рис.30); a,d – границы интервала, в котором существует вероятность наступления ошибок первого рода;

F(Δ) – функция распределения действительных значений погрешности средств измерений;

-∞,p – границы интервала, в котором погрешность средств измерений не препятствует наступлению ошибки первого рода.

Величина ошибки второго рода рассчитывается по формуле.

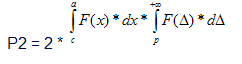
где с,a – границы интервала, в котором существует вероятность наступления ошибок второго рода;

p,+∞ – границы интервала, в котором погрешность средств измерений не препятствует наступлению ошибки второго рода.

Если предположить, что функция распределения значений погрешности средства измерений (FΔ) подчиняется закону нормального распределения, а  р равняется среднему значению погрешности, то будет верно выражение.

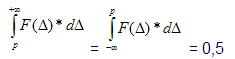
Практически расчет ошибок первого и второго рода по формулам (5, 6) на основании результатов измерений затруднителен в обычных условиях.